Indian National Olympiad in Informatics

Related:

Online Programming Contest, 9-10 July 2005

IARCS home > OLYMPIAD

Advanced Division

Problem 1: The Control Centre, (K Narayan Kumar, CMI)

The town of Siruseri has an excellent network of railway tracks on which runs one of the best suburban train systems in the country. The railway network is connected -- that is, one can go from any station to any other station. Further there is exactly one way of doing this if one does not visit any station twice.

The tracks and trains are maintained by an excellent team of technicians. The local government has decided to fund a state-of-the-art control centre for this railway network which will not only monitor the running of the network but also act as the base station for the technical team.

At which station should the control centre be located? Clearly, it should be chosen so that the time taken by the technical team to respond to any problem is minimized. So the authorities would like to identify the station for which the maximum distance from the other stations is minimized.

Suppose the railway map of Siruseri is as follows:

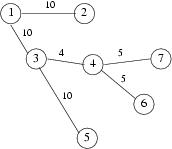
If the control centre is located at station 4 then the maximum distance is to station 2 (24 units). But if the control centre is located either at the station 1 or 3 the maximum distance to any other station is 20. You can verify that it is not possible to do better than this.

Your task is to take a description of the railway lines at Siruseri and identify the best choice for the control centre -- the station that minimizes the maximum distance to all other stations. You should also calculate the maximum distance between the station you have chosen and the other stations in the network.

Input format

The first line contains a single integer N indicating the number of stations in Siruseri. This is followed by a description of the distances between adjacent pairs of stations. Each line consists of 3 integers, A, B and W, where A and B are adjacent stations and W is the distance between them.

Output format

A single line containing two integers, the location of the control centre and the maximum distance between the control centre and all other stations. If there is more than one station where the control centre can be located, it suffices to print any one.

Test Data:

You may assume that N ≤ 100000. You may also assume that for any station, the number of neighbouring stations is bounded by 25. You may further assume that in 30% of the inputs N ≤ 5000.

Example:

Here is the sample input and output corresponding to the example discussed above.

Sample Input

Sample Output

3 20