Indian National Olympiad in Informatics

Related:

Online Programming Contest, 8-9 October 2005

IARCS home > OLYMPIAD

Advanced Division

Problem 1: Surveillance Cameras, (K Narayan Kumar, CMI)

A number of government offices are located at the centre of Siruseri. In the summer the temperatures in Siruseri tend to be intolerably high and so the government has decided to connect these offices by tunnels under the ground so that one can walk between buildings without having to step out into the heat.

Each building has a basement and the tunnels are accessed through these basements. Each tunnel connects a pair of buildings and no two tunnels intersect. The task of designing these tunnels was given to a well known architect. But as architects usually do, he indulged in his fancies. In his design, none of the tunnels are straight! Each tunnel consists of two straight segments and no two such segments are along the same line. Here is an example consisting of 4 offices and 4 tunnels:

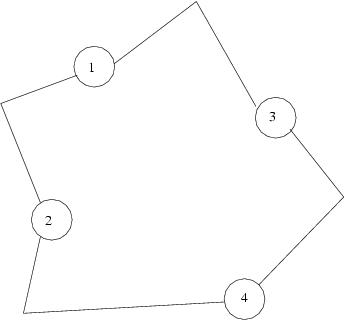
The Government has decided to install surveillance cameras in these tunnels. These cameras keep rotating and hence one camera may be able to periodically scan a number of (segments) of the tunnels. The government would like to determine the minimum number of cameras that need to be installed so that every part of every tunnel is scanned periodically. It is quite evident that it makes no sense to place the cameras in places other than the basements and the pointed corners in the tunnels, since a camera placed in the middle of segment might as well be moved to either of its ends. In the above example, one can cover the entire network with 4 cameras, one each placed in each of the four basments. It can also be covered by placing 4 cameras one each at the pointed corners of each tunnel.

Your task is to write a program that takes in a description of the layout of buildings and tunnels and determines the minimum number of cameras that need to be purchased and the locations where they should be installed.

Input format

The first line of the input contains a two integers N and M where N is the number of buildings and M is the number of tunnels. This is followed by M lines each containing a pair of integers describing the endpoints of the M tunnels. You may assume that between any pair of buildings there is at the most one tunnel connecting them.

Output format

The first line of output must contain a single integer K indicating the number of cameras that need to be installed. This should be followed by K lines each containing either an integer i (indicating that a camera must be placed in the basement of building i) or a pair of space separated integers i and j (indicating that a camera should be placed at the pointed corner of the tunnel connecting buildings i and j). If there is more than one way to install the cameras then it suffices to print out any one.

Test Data:

You may assume that 1 ≤ N ≤ M ≤ 200000.

Example:

Here is the sample input and output corresponding to the example discussed above.

Sample Input

Sample Output